 1 2 Jump to
1 2 Jump to
| Theoretical Philosophy » Hume's Fork and mathematical knowledge » 8/21/2015 7:13 pm |
- Tyrrell McAllister
- Replies: 9
-
Hume would have to accept that math isn't "true about extra-mental reality", because it is about ideas, which exist only in minds. But he could still say that math is objective, in the same sense that there are objective truths about minds, even though these truths, trivially, aren't about extra-mental reality.
He has a problem with accounting how truths about "my idea of 2" could have anything to do with truths about "your idea of 2". (When my idea of squaring is combined with my idea of 2 in a certain way, I get my idea of 4. But this is supposed to reflect a truth about anyone's ideas, not just mine.) But this is a general problem. (In what sense is your idea of gold "the same as" my idea of gold?) It's not obviously a special problem for mathematical ideas.
| Theoretical Philosophy » Hume's Fork and mathematical knowledge » 8/21/2015 6:53 pm |
- Tyrrell McAllister
- Replies: 9
-
The criticism that I've heard of Russell and Whitehead is this: that they tried to show that mathematics was about, not just relations of ideas, but relations of purely logical ideas and nothing else. In particular, I've seen R&W criticised for trying to assimulate the idea of infinity to logic. Critics argue that the idea of infinity (as used in mathematics) is irreducibly mathematical and can't be reduced to pure logic.
Hume could evade this criticism, because, for him, the ideas in "relations of ideas" aren't restricted to logical ideas.
| Chit-Chat » Logic Resources » 8/06/2015 12:48 pm |
- Tyrrell McAllister
- Replies: 4
-
I got a lot out of Kneebone's Mathematical Logic and the Foundations of Mathematics. It's available in a very affordable Dover edition. (The one Amazon review is unfair, in my opinion. The professional reviews here give a far more accurate impression.)
The book is probably not suitable if you have no experience at all with formal logic, say up to quantified predicate logic. But even just a basic working knowledge of formal logic should be enough to make the text valuable. You should be good to go if you've ever drawn of up a truth table and converted a sentence of natural language into something like (∀x)((Px ∧ Qy) ⟹ (Rx ∨ (∃y)(Py ∧ Rxy))).
(That symbolic expression might formalize the following sentence: "No matter who you are, if you live in an apartment building and play loud music, then either you have no neighbors, or else there is an apartment-dweller out there who is plotting to cut off your electricity.")
| Practical Philosophy » What is it to "Oppose" an Organ's Natural Function? » 8/06/2015 11:39 am |
- Tyrrell McAllister
- Replies: 26
-
I also am having trouble grasping "perverted faculty" arguments. I think that my difficulty centers around the term "faculty".
What exactly is a "faculty" in A-T? Are the terms "power" and "capacity" synonymous with "faculty" in this context? Where exactly should I situate faculties in my "A-T metaphysical mental model"?
More generally, there are several subtleties of "faculty-speak" that I don't yet grasp. For example, I was taken aback with Scott wrote, Scott wrote:
Scott wrote:Objectively, it is the "reproductive faculty" that is being used in (male) masturbation, and it can't very well be otherwise if the outcome is ejaculation.
Now, I get that the reproductive organs are being used. I get that these organs are being used in a way that frustrates their purpose, which is to play their part in reproduction. But in what sense is the reproductive faculty being used? Certainly, the owner did not in fact reproduce. I suppose that I assumed that a faculty, to be used, must be used successfully. Analogously, you can't use your faculty of sight with a blindfold on. You can only try to use that faculty, but your attempt will fail, so that, in the end, the faculty remains unused. At least, that's how I'm inclined to use the language in that case.
Could someone recommend a text that gives the A-T position on the metaphysics of faculties in general (not just in the context of their perversion)?
| Theoretical Philosophy » Hume's Fork and mathematical knowledge » 8/05/2015 6:23 pm |
- Tyrrell McAllister
- Replies: 9
-
A few times, Feser has said that Hume's Fork fails to account for mathematical knowledge, because mathematical knowledge is about neither "matters of fact" nor "relations of ideas".
This criticism puzzles me, because mathematical knowledge is Hume's paradigmatic example of knowledge concerning "relations of ideas". Insofar as we know what Hume meant by the phrase "relations of ideas" at all, it is because he said that these relations are what mathematical knowledge is about. From his first Enquiry: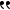 Hume wrote:
Hume wrote:ALL the objects of human reason or enquiry may naturally be divided into two kinds, to wit, Relations of Ideas, and Matters of Fact. Of the first kind are the sciences of Geometry, Algebra, and Arithmetic; and in short, every affirmation which is either intuitively or demonstratively certain. That the square of the hypotenuse is equal to the square of the two sides, is a proposition which expresses a relation between these figures. That three times five is equal to the half of thirty, expresses a relation between these numbers. Propositions of this kind are discoverable by the mere operation of thought, without dependence on what is anywhere existent in the universe. Though there never were a circle or triangle in nature, the truths demonstrated by Euclid would for ever retain their certainty and evidence.
Literally all of the examples here of knowledge concerning relations of ideas are mathematical. It's not much of an exaggeration to say that Hume is giving an ostensive definition; it's as if he wrote "You know that kind of knowledge that you get when you gain mathematical knowledge? That's what I'm calling knowledge concerning relations of ideas"
…
Hume might not mean for the phrases "knowledge concerning relations of ideas" (or "KCRI", for short) and "mathematical knowledge" to be synonymous. Maybe Hume acknowledges some non-mathematical knowledge that is still KCRI. Perhaps Hume can justly be criticized for obsc
| Religion » Original sin and von Neumann machines » 7/11/2015 5:47 pm |
- Tyrrell McAllister
- Replies: 7
-
Well, if you're not, the Catechism trumps him anyway
I don't think that my reading of Aquinas contradicts the Catechism (as I read it). But that's only because I wasn't reading a very particular meaning into the word "guilt". My understanding of what Aquinas meant by the word was too vague to be easily contradicted.
You mention the distinction between individual and corporate guilt. This raises the question for me of just what either of these kinds of guilt are. For example, when a father commits a crime, and his son inherits corporate guilt, is this guilt a feature of the son himself, or is it just a relational fact about how other people perceive him (e.g., as somehow "stained" by his father's crime)? If no one knew that the son was related to the father, would he still share in corporate guilt in any objective sense?
(It probably goes without saying, but I'm looking for answers from the perspective of scholasticism.)
| Religion » Original sin and von Neumann machines » 7/08/2015 10:58 am |
- Tyrrell McAllister
- Replies: 7
-
 Scott wrote:
Scott wrote:One caveat: be careful in speaking of "guilt," as the Church specifically denies that any personal "original guilt "associated with original sin is somehow inherited (just the state of original sin, namely the privation of sanctifying grace).
If I'm reading Aquinas correctly, guilt associated with original sin is inherited, but this guilt is washed away by baptism (without repairing the "damage"). Here are the lines that give me this impression (from the link that I gave in the OP):
"[i]n the case before us ... guilt is transmitted by the way of origin from father to son, even as actual sin is transmitted through being imitated."
"[H]e that is born is associated with his first parent in his guilt, through the fact that he inherits his nature from him by a kind of movement which is that of generation."
"Although the guilt is not actually in the semen, yet human nature is there virtually accompanied by that guilt."
"Original sin is taken away by Baptism as to the guilt, in so far as the soul recovers grace as regards the mind."
Am I misunderstanding Aquinas on the heritability of Adam's guilt?
| Religion » Original sin and von Neumann machines » 7/07/2015 7:44 pm |
- Tyrrell McAllister
- Replies: 7
-
I've been reading Summa Theologica, First Part of the Second Part, Question 81, Article 1: "Whether the first sin of our first parent is contracted by his descendants, by way of origin?" ()
…
In an effort to test my understanding, I'm trying to rephrase Aquinas's position in terms of von Neumann machines. This is probably a little kooky. I'm wondering if it is at all on the right track. (I have no emotional attachment to this, so feel free to tear it to shreds.)
The picture that I'm getting is something like the following: Human Nature is like a computer program. Adam was like a von Neumann machine that ran the first instance of this program, and who built subsequent instances. A soul is a particular instantiation of this program in an individual machine. Original sin came into the program itself, and hence into Adam, and hence into each of us via Adam because he built the machines that built the machines that ... that built the machines that built us.
(I'm calling us "machines" here just because I'm thinking of us as like von Neumann machines in some sense for purposes of illustration. I realize that we are not literally machines under A-T.)
The point is, it was the program, the nature common to us all, that sinned, and not just the particular instance of the program in Adam. That is how each of us can have guilt.
This raises the question of when the damage to the nature occurred. At first, it seems that, if Adam's nature had changed from undamaged to damaged after he was alive, then he would have changed his substantial form and so become a different kind of thing. That is, he would have been destroyed at the time of his sin and replaced by something else of a different kind. But this doesn't seem like the intended story.
This suggests that there is an "inner program" and an "outer program". The inner program is the substantial form itself, which cannot change, any more than the form of "triangle
| Theoretical Philosophy » Common misconceptions about Scholasticism » 7/07/2015 7:11 pm |
- Tyrrell McAllister
- Replies: 12
-
Here are a couple more misconception about Scholasticism. At least, these are things that I used to believe:
(1) One misconception is that scholastics were routinely fooled by pseudo-explanations like Molière's parody answer to "Why does opium cause sleep?" Namely, "Because of its soporific power."
(2) There is an exaggerated notion of the extent to which false beliefs about the natural world are logical consequences of scholastic metaphysics. For example, the fact that bodies throughout the universe don't tend towards the center of the Earth is thought to falsify something in scholastic metaphysics.
| Introductions » Hello » 7/07/2015 6:47 pm |
- Tyrrell McAllister
- Replies: 3
-
Hello, everyone.
I am a mathematician with an amateur interest in philosophy. For several years now, I've been learning a lot from Feser's posts and from the helpful and knowledgeable commentors that his blog attracts. I'm excited to see that some of these commentors are starting a free-standing forum here.
My own philosophical outlook, both by nature and on reflection, is atheistic, materialistic, and reductionistic. In other words, from the A-T standpoint, wrong, wrong, wrong! So I've always appreciated the patience with which my questions have been answered by the commentors on Feser's blog. Thanks to them, I have some glimmering of the monumental intellectual power of the A-T ediface. If I am indeed radically wrong in my worldview, then A-T, among all the systems that I know, seems most likely to be right. I'm looking forward to learning more about this system here.
 1 2 Jump to
1 2 Jump to